Paradox in Hit And Blow
- Using Items
- Calculate Candidates Programmatically
- Then... what's the paradox?
- Expectation Value
- Shot Expectation Value

Today, I'm going to introduce a paradox I discovered while playing a game 'Hit and Blow.'
IThe game revolves around guessing a sequence of three numbers (sometimes four numbers) set by another player. The objective is to deduce the correct three-digit number through a series of guesses. After each guess, the opposing player provides feedback in the form of 'hits' and 'blows.' A 'hit' indicates that one of the guessed numbers is correct and in its right position, while a 'blow' signifies that a guessed number is correct but placed in the wrong position. The paradox I came across emerged from the game's unique logic and the strategies used to guess the correct number sequence, which led to an unexpected and intriguing challenge that deviates from the standard approach usually taken in this game. And we cannot include same number in the game. So 001, 556, or 333 are not allowed.
For example, let's say the secret number sequence set by the other player is "482". In my first guess, I might try "123". The feedback I receive is "1 blow," indicating that one of these numbers is correct but in the wrong position. None of the numbers are in the correct position, so there are no hits.

Based on a sequence of this guessing process, both the player and their opponent, engage in a strategic battle of wits. Each participant takes turns to guess the three-digit number secretly set by the other. The game continues in this back-and-forth manner, with each player using the received clues to get closer to the correct sequence. The winner of the game is the first player who successfully guesses the opponent's number sequence accurately, achieving 3 hits.

Using Items
In Hit and Blow, players have access to four unique types of items that aid in deducing the opponent's secret number.
High/Low: This item reveals whether each digit of the opponent's number is 'High' (5-9) or 'Low' (0-4). For example, if the result is "HHL," it indicates that the first digit is in the range of 5-9, the second could be either high or low, and the third is definitely between 0-4. This information helps narrow down the possibilities, as seen in numbers like 560, 893, or 762, where the first digit is high, the second could be high or low, but the third is low.
Shot: This item allows players to guess a specific digit and learn if it's included in the opponent's number and its exact position. For instance, choosing '5' with a 'Shot' item and discovering the opponent's number is 851 would reveal that '5' is the second digit.
Shuffle: With the 'Shuffle' item, players can rearrange the digits in their own guessed number. This can be strategically used to test different combinations and see how the feedback changes, helping to refine further guesses.
Change: The 'Change' item enables players to alter one digit of their guessed number. However, it comes with a restriction: the new digit must remain within the same 'High' or 'Low' category as the original. For example, if a player’s current number is 025 and they choose to change the first digit '0', they can only replace it with other 'Low' digits like 1, 3, or 4, but not with a 'High' digit.
These items add an extra layer of strategy to the game, allowing players to gather more information and make more informed guesses about their opponent's secret number.
Calculate Candidates Programmatically
Following the introduction of these strategic items, players can further enhance their gameplay by programmatically calculating the possible candidates for the opponent's number.
This method involves using the feedback from each guess, along with the insights gained from the items, to systematically narrow down the list of potential numbers. By applying logical deductions and algorithms, players can efficiently eliminate unlikely combinations and focus on the most probable ones.
This approach not only streamlines the guessing process but also introduces a more analytical and methodical aspect to the game. The blend of strategic item usage and programmatic calculation creates a dynamic and intellectually stimulating experience, making each round of Hit and Blow not just a game of luck but a test of logic and strategic planning.
Below code snippet is designed to generate all possible combinations of three-digit numbers, ranging from 012 to 987, without any repeated digits in each number. Initially, it creates a comprehensive list of numbers using the allCandidates function, which constructs every three-digit combination by padding shorter numbers with leading zeros. Subsequently, the removeDuplicatedNumbers function filters this list to exclude any numbers containing duplicate digits. By leveraging a Set in TypeScript, the code efficiently identifies and removes numbers with repeated digits, ensuring each digit in a number is unique. The result is a refined list of all valid three-digit combinations where each digit is distinct, an essential dataset for strategies in games like Hit & Blow.
const allCandidates = (n: number): number[][] => { const possibleNumbers = Array.from({ length: 10 ** n }, (_, i) => String(i) .padStart(n, "0") .split("") .map((x) => parseInt(x)) ); const filteredNumbers = removeDuplicatedNumbers(possibleNumbers); return filteredNumbers; }; function removeDuplicatedNumbers(array: number[][]): number[][] { return array.filter((digits) => { const uniqueDigits = new Set(digits); // Create a set from those digits return uniqueDigits.size === digits.length; // Compare the size of the set to the length of the digits array }); }
And we obtain all possible candidates at first of the game.
console.log(allCandidates(3).map((cand) => cand.join(""))); // ["012", "013", "014", "015", "016", "017", "018", "019", "021", "023", "024", "025", "026", "027", "028", "029", "031", "032", "034", "035", "036", "037", "038", "039", "041", "042", "043", "045", "046", "047", "048", "049", "051", "052", "053", "054", "056", "057", "058", "059", "061", "062", "063", "064", "065", "067", "068", "069", "071", "072", "073", "074", "075", "076", "078", "079", "081", "082", "083", "084", "085", "086", "087", "089", "091", "092", "093", "094", "095", "096", "097", "098", "102", "103", "104", "105", "106", "107", "108", "109", "120", "123", "124", "125", "126", "127", "128", "129", "130", "132", "134", "135", "136", "137", "138", "139", "140", "142", "143", "145", "146", "147", "148", "149", "150", "152", "153", "154", "156", "157", "158", "159", "160", "162", "163", "164", "165", "167", "168", "169", "170", "172", "173", "174", "175", "176", "178", "179", "180", "182", "183", "184", "185", "186", "187", "189", "190", "192", "193", "194", "195", "196", "197", "198", "201", "203", "204", "205", "206", "207", "208", "209", "210", "213", "214", "215", "216", "217", "218", "219", "230", "231", "234", "235", "236", "237", "238", "239", "240", "241", "243", "245", "246", "247", "248", "249", "250", "251", "253", "254", "256", "257", "258", "259", "260", "261", "263", "264", "265", "267", "268", "269", "270", "271", "273", "274", "275", "276", "278", "279", "280", "281", "283", "284", "285", "286", "287", "289", "290", "291", "293", "294", "295", "296", "297", "298", "301", "302", "304", "305", "306", "307", "308", "309", "310", "312", "314", "315", "316", "317", "318", "319", "320", "321", "324", "325", "326", "327", "328", "329", "340", "341", "342", "345", "346", "347", "348", "349", "350", "351", "352", "354", "356", "357", "358", "359", "360", "361", "362", "364", "365", "367", "368", "369", "370", "371", "372", "374", "375", "376", "378", "379", "380", "381", "382", "384", "385", "386", "387", "389", "390", "391", "392", "394", "395", "396", "397", "398", "401", "402", "403", "405", "406", "407", "408", "409", "410", "412", "413", "415", "416", "417", "418", "419", "420", "421", "423", "425", "426", "427", "428", "429", "430", "431", "432", "435", "436", "437", "438", "439", "450", "451", "452", "453", "456", "457", "458", "459", "460", "461", "462", "463", "465", "467", "468", "469", "470", "471", "472", "473", "475", "476", "478", "479", "480", "481", "482", "483", "485", "486", "487", "489", "490", "491", "492", "493", "495", "496", "497", "498", "501", "502", "503", "504", "506", "507", "508", "509", "510", "512", "513", "514", "516", "517", "518", "519", "520", "521", "523", "524", "526", "527", "528", "529", "530", "531", "532", "534", "536", "537", "538", "539", "540", "541", "542", "543", "546", "547", "548", "549", "560", "561", "562", "563", "564", "567", "568", "569", "570", "571", "572", "573", "574", "576", "578", "579", "580", "581", "582", "583", "584", "586", "587", "589", "590", "591", "592", "593", "594", "596", "597", "598", "601", "602", "603", "604", "605", "607", "608", "609", "610", "612", "613", "614", "615", "617", "618", "619", "620", "621", "623", "624", "625", "627", "628", "629", "630", "631", "632", "634", "635", "637", "638", "639", "640", "641", "642", "643", "645", "647", "648", "649", "650", "651", "652", "653", "654", "657", "658", "659", "670", "671", "672", "673", "674", "675", "678", "679", "680", "681", "682", "683", "684", "685", "687", "689", "690", "691", "692", "693", "694", "695", "697", "698", "701", "702", "703", "704", "705", "706", "708", "709", "710", "712", "713", "714", "715", "716", "718", "719", "720", "721", "723", "724", "725", "726", "728", "729", "730", "731", "732", "734", "735", "736", "738", "739", "740", "741", "742", "743", "745", "746", "748", "749", "750", "751", "752", "753", "754", "756", "758", "759", "760", "761", "762", "763", "764", "765", "768", "769", "780", "781", "782", "783", "784", "785", "786", "789", "790", "791", "792", "793", "794", "795", "796", "798", "801", "802", "803", "804", "805", "806", "807", "809", "810", "812", "813", "814", "815", "816", "817", "819", "820", "821", "823", "824", "825", "826", "827", "829", "830", "831", "832", "834", "835", "836", "837", "839", "840", "841", "842", "843", "845", "846", "847", "849", "850", "851", "852", "853", "854", "856", "857", "859", "860", "861", "862", "863", "864", "865", "867", "869", "870", "871", "872", "873", "874", "875", "876", "879", "890", "891", "892", "893", "894", "895", "896", "897", "901", "902", "903", "904", "905", "906", "907", "908", "910", "912", "913", "914", "915", "916", "917", "918", "920", "921", "923", "924", "925", "926", "927", "928", "930", "931", "932", "934", "935", "936", "937", "938", "940", "941", "942", "943", "945", "946", "947", "948", "950", "951", "952", "953", "954", "956", "957", "958", "960", "961", "962", "963", "964", "965", "967", "968", "970", "971", "972", "973", "974", "975", "976", "978", "980", "981", "982", "983", "984", "985", "986", "987"]
From this candidates, we need to think how should we narrow down from this massive amount of numbers to certain elaborated array.
But ah....... in this time, I will skip to write down this logic😐
Because this article is intending to just introduce paradox, and actually it's not relating to Hit and Blow algorithms itself, but "Shot" item.
Then... what's the paradox?
"Shot" item, which I described in above can narrow down candidates by judging whether chosen number is included in the opponent's one or not. And determine where the number is.
Let's consider about an example of candidates (670, 680, 690, 750, 850, 950). We can see there is 6 at the first half of array and there isn't in the second half. And same about 5 too.
When we shot 0, nothing happened because every candidates contain 0 at the same place.
When we shot 6, candidates will be (670, 680, 690) if opponent's one is included in this 3 numbers. And if not, they will be (750, 850, 950) instead.
It seems obviously better than when we shot 0, because shot 0 can't narrow down anything!
.........But is it really true?
Actually, it's not true.
It must be paradoxical because when we narrow candidates down from 6 to 3, merely the probability to answer is increased from 1/6 to 1/3.
But actually, there is no difference between shot 0 and shot 6, in this case, when we consider "How fast we can win".
Expectation Value
The probability of winning a game is not determined by the immediate chance of correctly answering a target, but rather by the expected value of the total number of answers over time.
Let's define this as ], where
represents the total number of answers over time. Consider
as the set of candidates, with
, where
denotes the size of set
.
Given the current set of candidates , and assuming the next input is
, we need to calculate the expected value of the total number of answers over time, represented as
]. Since each candidate has an equal probability of being the correct answer,
] can be calculated as the average of
], ...,
]:
\begin{eqnarray}E[T] &=& \frac{1}{N} \sum^{N}_{i=1} T(c_i, \mathbf{c}) \newline &=& \frac{1}{N} \sum^{N}_{i=1} E[T(c_i, \mathbf{c})]\end{eqnarray}
The reason why the average of is equal to the average of
] is due to the nature of the expected value and the uniform probability of each candidate being the correct answer.
If the length of candidates is 1, it's obvious that this expectation value must be 0 because we already know the answer.
Also, if length is 2, expectation value must be 0.5 because when , we won answer if we input
and actual answer is
too. But we need to answer once more when actual answer is
. So expectation value
] must be (0+1)/2 = 0.5. Same logic remains if input is
. So we obtain expectation value as (0.5 + 0.5)/2 = 0.5.
Considering this example, we can calculate ] by this equation with some function
:
\begin{align}E[T(c_i, \mathbf{c})] = \frac{1}{N} \sum^{N}_{j=1} U(c_i, \mathbf{c}^{\ast}_{ij})\end{align}
Where is the new candidates assuming actual opponent's number(answer) is
and when the input is
.
For example, let
be (670, 680, 690, 750, 850, 950) again. And if our next input
is 670, assuming opponent's actual number
is 850, hits and blows are 1, 0 respectively. So we obtain (850, 950) as the new candidates
that satisfies hits 1, blows 0 against 670.
Such way of thinking is similar to calculating entropy in information theory.
Then, what should be? We just can say it's different from
at least.
But actually, this can be expressed as below:
\begin{align}U(c_i, \mathbf{c}^{\ast}_{ij}) = 1 + T(c_i, \mathbf{c}^{\ast}_{ij})\end{align}
This is because when looking at , we are not considering the next input yet, but just certain current input is
and new candidates is
. So we just need to plus 1 to T.
Thus, previous equation become
\begin{eqnarray}E[T(c_i, \mathbf{c})] &=& 1 + \frac{1}{N} \sum^{N}_{j=1} T(c_i, \mathbf{c}^{\ast}_{ij}) \newline &=& 1 + \frac{1}{N} \sum^{N}_{j=1} E[T(c_i, \mathbf{c}^{\ast}_{ij})\end{eqnarray}
Then finally, we obtain a recurrence formula of ].
Shot Expectation Value
Next we have to compare each shot's efficacy.
We calculate expectation value again, but against shot.
At first, fixing constant shot target number , calculate new candidates of the case of shot each places
from original candidates
, then calculate
]
of each new candidates. After calculation of each
], we obtain expectation value of the total number of answers over time after shot n
as
\begin{align} E[S_n] = \frac{1}{|\mathbf{c}|} \sum_{place} |\mathbb{c}^{\ast}_{place}| * E[T]_{place} \end{align}
This figure is a concrete example of shot 7.

Finally, using same algorithm, we obtain

as the result.
This means that how we take advantages after shot 0 and shot 6 in this case -though shot 6 narrow candidates down to half than shot 0- have no difference.
Because, whether you can win a game is determined not by the temporary probability of answering a target, but by the expected value of the total number of answers over time.
\begin{align}\end{align}
10x Faster Collatz Calculation
A New Insight into the Collatz Conjecture
In the vast domain of mathematics, the Collatz conjecture holds its unique intrigue. A few days ago, I made an observation that the maximum curve of the Collatz total stopping time bears a resemblance to that of a logarithmic function. This revelation piqued my interest and led me to think: Could there be a more efficient way to calculate the Collatz operation? Traditional methods have been effective in exploring its patterns, but with this new insight, I felt compelled to seek out a method that could potentially expedite the calculations. This article delves into a method that has empirically shown to calculate the Collatz sequence up to 10 times faster than conventional techniques.
Traditional Collatz Sequence Computation
Traditionally, the computation of the Collatz sequence involves the following iterative process:
- Start with any positive integer
n. - If
nis even, divide it by 2: \begin{align}n \rightarrow \frac{n}{2}\end{align} - If
nis odd, multiply it by 3 and add 1: \begin{align} n \rightarrow 3n + 1 \end{align} - Repeat the process with the new value of
n, untilnbecomes 1.
This method is straightforward but involves many iterations, especially for numbers that require a large number of steps to reach 1. For instance, numbers that take hundreds or even thousands of steps can make the process quite slow. Each step in the process requires a calculation, and as the starting number increases, the potential number of steps can grow significantly. This approach, while effective, can be time-consuming, especially for large numbers and extensive ranges.
This is a sample python code up to N = 1,000,000 (Note that this is originally for verifying my hypotheses):
### Traditional Method import matplotlib.pyplot as plt import numpy as np import time def collatz(n): if n % 2 == 0: return int(n/2) else: return 3*n+1 def collatz_seq(n): result = [n] while n > 1: n = collatz(n) result.append(n) return result def plot_collatz(max_n): x = list(range(1, max_n)) y = [len(collatz_seq(i)) for i in x] # Filter x and y to keep only points where y is a new maximum max_y = 0 new_x, new_y = [], [] for i, val in enumerate(y): if val > max_y: max_y = val new_x.append(x[i]) new_y.append(val) # Generate the logarithmic data log_y = [3 * np.log(val)**2 for val in x] plt.figure(figsize=(10, 6)) plt.scatter(new_x, new_y, color='blue', label='Collatz Data') plt.plot(new_x, new_y, color='blue', marker='o') plt.plot(x, log_y, color='red', label='Logarithmic Function') plt.title(f"Comparison between Collatz sequences and Logarithmic function (n={max_n})") plt.xlabel("Number") plt.ylabel("Value") plt.grid(True, which='both', linestyle='--', linewidth=0.5) plt.legend() plt.show() # Plotting for each value start_time = time.time() for n in [1000000]: plot_collatz(n) end_time = time.time() execution_time = end_time - start_time print(f"The execution time is {execution_time} seconds.")
This yields:

You can see that this traditional way takes time about 1 minute.
10x Faster Collatz Sequence Computation
One of the foundational elements that has significantly accelerated the computation is the use of caching. In programming, caching is a technique where previously computed results are stored for quicker access in subsequent runs. If the same computations are required again, instead of recalculating them, the program fetches the stored result.
In the given code, caching is achieved using a dictionary named collatz_dic. This dictionary acts as our cache. Whenever we compute the total stopping time for a number n, before moving further in the sequence, the code checks if n already exists in collatz_dic. If it does, it means we have previously calculated the stopping time for that number and we can simply fetch the result from the dictionary instead of recalculating it.
if n in collatz_dic: result = collatz_dic[n] break
This simple check and retrieval mechanism drastically reduces the computation time as the number of Collatz operations decreases with each known value we encounter.
To ensure that the cache keeps updating and becomes more efficient with every run, new numbers encountered during the calculation, which aren't in the cache, are stored in a list named newNumbers. After the sequence breaks, we populate the collatz_dic with these new numbers and their respective stopping times:
len_newNumbers = len(newNumbers) for i in range(1, len_newNumbers): result += 1 collatz_dic[newNumbers[len_newNumbers - i]] = result
By utilizing this approach, the calculation time was observed to decrease significantly, making it up to 10 times faster. This isn't just a theoretical improvement; the reduction in computational time has practical implications, especially for intensive research and larger datasets.
Efficiency in mathematical computations is always a sought-after goal. By exploring alternative methods and continuously refining our approaches, we can uncover more efficient ways to understand and solve problems. The alternative method for the Collatz sequence computation is a testament to this endeavor. While the journey in understanding the Collatz conjecture is far from over, innovations like these bring us a step closer to more profound insights.
This is the sample python code:
import matplotlib.pyplot as plt import numpy as np import time collatz_dic = {} def collatz(n): if n % 2 == 0: return int(n/2) else: return 3*n+1 def collatz_total_stopping_time(n): newNumbers = [] result = 0 while n > 1: if n in collatz_dic: result = collatz_dic[n] break else: newNumbers.append(n) n = collatz(n) len_newNumbers = len(newNumbers) for i in range(1, len_newNumbers): result += 1 collatz_dic[newNumbers[len_newNumbers - i]] = result return result def plot_collatz(max_n): x = list(range(1, max_n)) y = [collatz_total_stopping_time(i) for i in x] # Filter x and y to keep only points where y is a new maximum max_y = 0 new_x, new_y = [], [] for i, val in enumerate(y): if val > max_y: max_y = val new_x.append(x[i]) new_y.append(val) # Generate the logarithmic data log_y = [3 * np.log(val)**2 for val in x] plt.figure(figsize=(10, 6)) plt.scatter(new_x, new_y, color='blue', label='Collatz Data') plt.plot(new_x, new_y, color='blue', marker='o') plt.plot(x, log_y, color='red', label='Logarithmic Function') plt.title(f"Comparison between Collatz sequences and Logarithmic function (n={max_n})") plt.xlabel("Number") plt.ylabel("Value") plt.grid(True, which='both', linestyle='--', linewidth=0.5) plt.legend() plt.show() # Plotting for each value start_time = time.time() for n in [1000000]: plot_collatz(n) end_time = time.time() execution_time = end_time - start_time print(f"The execution time is {execution_time} seconds.")
This yields:
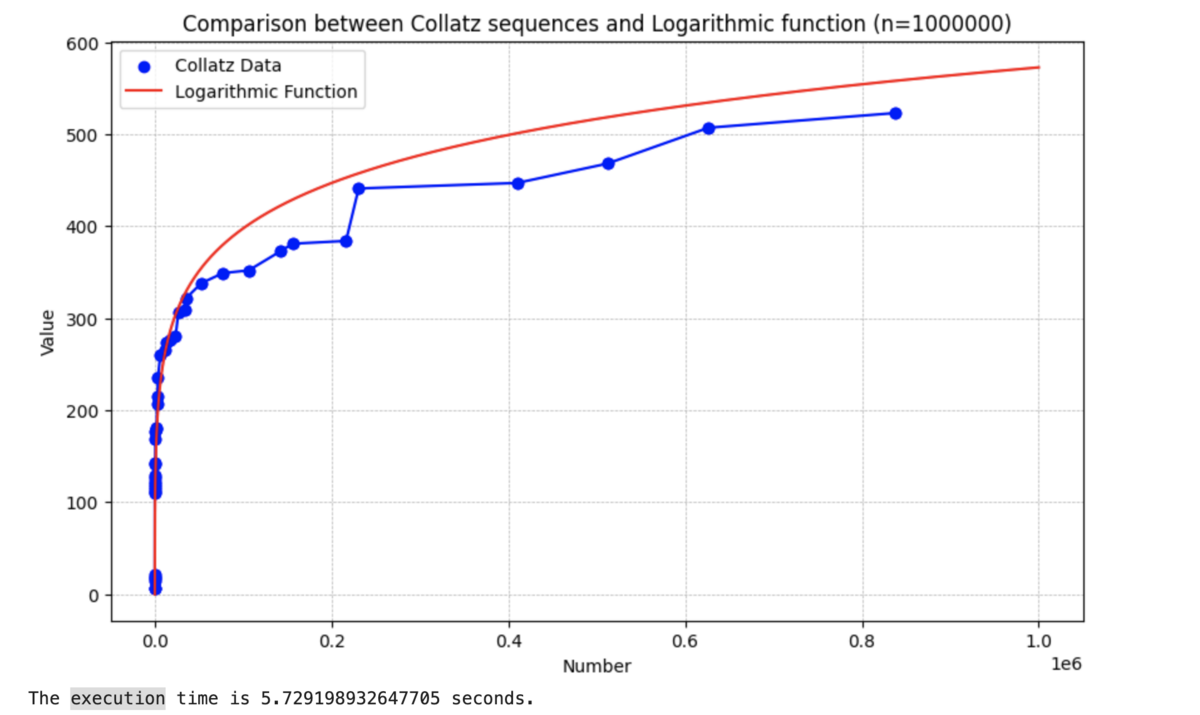
And this only takes 6 seconds. Which is 10 times faster than the traditional way.
Conclusion
The Collatz conjecture, with its seemingly simple rules, continues to puzzle and captivate mathematicians worldwide. Through this article, we've introduced a more efficient computational approach that utilizes caching, which has empirically demonstrated significant speed improvements over traditional methods.
My observation of the curve of the Collatz total stopping time bearing resemblance to the curve of a squared logarithm isn't just a fleeting observation but forms the basis of my hypothesis. It is my fervent hope that someday this hypothesis can be rigorously validated, potentially paving the way for a deeper understanding of the Collatz sequence.
Drawing from the rich theories of zeta functions – a cornerstone of my academic pursuits – and the intricate realms of algebraic structures like Galois theory, I believe we might find clues that will bring us closer to a solution. These mathematical avenues might not only elucidate the Collatz conjecture but also enrich our understanding of the broader tapestry of number theory.
As we continue to unravel the intricacies of the Collatz sequence, the convergence of computational techniques and profound mathematical theories will undoubtedly play a pivotal role. Here's to hoping that the combination of empirical observation, analytic methods, and algebraic structures will someday bear fruit in our quest to decipher the enigma of the Collatz conjecture.
電磁気学の備忘録

みやすさ重視で雑ですがあしからず———
クーロンの法則、ビオサバールの法則、ローレンツ力
電場、
電束密度
磁場、
磁束密度
クーロンの法則(Coulomb's law)
荷電粒子間にはたらく電場は電荷量に比例し、距離の二乗に反比例する。
\begin{align}
\boldsymbol{E}=\frac{q}{4\pi \varepsilon_0}\frac{\hat{\boldsymbol{r}}}{|\boldsymbol{r}|^2}
\end{align}
ここで]は真空誘電率(permittivity of vacuum)
話はそれるが、permit は透過する・通過するという意味があるのでそれに能率という意味をもつ ~tivityをつけることで permittivity になるんだなあ。一見ややこしい英単語も語源に着目すれば簡単に覚えられる。
ビオ・ザバールの法則(Biot–Savart law)
微小な長さの電流要素によって
離れた位置に作られる微小な磁束密度
は
\begin{align}
d\boldsymbol{B}=\frac{\mu_0 I}{4\pi}\frac{d\boldsymbol{l}\times \hat{\boldsymbol{r}}}{|\boldsymbol{r}|^2}
\end{align}
ここで]は真空透磁率(permeability in vacuum)で、
である。
permit には透過するという意味があるけど、さらに語源をたどると per にもそのような意味があるので同様に、能力という意味を持つ ability を付け加えて per me abillity になるんだろうなあというのは分かるんだけど、真ん中の me はなんだろう? 多分「磁」という意味に近いんだろうと思う。だとしても magnet が me になるか。。。?
ローレンツ力(Lorentz force)
電磁場中で運動する荷電粒子が受ける力は
\begin{align}
\boldsymbol{F}=q(\boldsymbol{E}+\boldsymbol{\upsilon}\times\boldsymbol{B})
\end{align}
「この世界がそのような物理法則を選んだから。」で済ませられるかもしれないが、それでも粒子の動く向きと磁束密度(磁場)の向きにわざわざ垂直になるように対して力が発生しなければならないというのは、不思議な感覚である。
余談だけど、トリック1の4話で、村から人が消えるという怪奇現象について尋ねられた上田次郎が、適当にローレンツ力の説明をして、「それじゃ鍋とか木も消えてないとおかしくないべか?」みたいなツッコミをされていたのが印象的だった。トリックはシーズン1だけでも3周した。なつかしい。。。 *1
ガウスの定理、ストークスの定理
ベクトル場に対して
ガウスの定理(Gauss' theorem, divergence theorem)
\begin{align}
\int \rm{div} \boldsymbol{E}\ dV = \int \boldsymbol{E}\cdot \boldsymbol{n}\ dS
\end{align}
ストークスの定理(Stokes' theorem)
\begin{align}
\int \rm{rot} \boldsymbol{E}\cdot \boldsymbol{n}\ dS = \int \boldsymbol{E}\cdot d\boldsymbol{s}
\end{align}
体積分を面積分に、面積分を線積分へと変換することができる式だ。空間に対して連続的に変化するベクトル場という概念だからこそ成り立つ式だろう。ガウスの定理はつまり、とある体積内での場の発散は、その境界面においての場の法線成分を足し合わせることでできるということであるが、一度図として理解するととても当たり前のことのように感じる。もし人類より知能の高い宇宙人がいるとしたら、これくらいの積分は計算するまでもなく直感で導き出せてしまうのかもしれない。*2
ストークスの定理は同様に、とある曲面での場の回転の法線成分を足し合わせたものというのは、そのフチでの場の成分をフチにそって足し合わせたものと等しくなるということで、これも一度図で理解すればその理由が容易に理解できる。というかこれはウィトゲンシュタインのいう単なる言語ゲームで、最初は式の意味がわからないのはそれは式の構成要素、つまり単語の意味についての認識が不十分だからで、一度図を書くなり調べるなりして自分の中でその単語の意味についての正しい認識を固めていくことで、単語について理解したときには式の意味も理解できるようになっているというだけのことなのかもしれない。
マクスウェルの方程式
マクスウェルの方程式(Maxwell's equations)
\begin{align}
\rm{div} \boldsymbol{E} &= \frac{\rho}{\varepsilon_0}\\
\rm{div}\boldsymbol{B} &= 0\\
\rm{rot} \boldsymbol{E} &= -\frac{\partial\boldsymbol{B}}{\partial t}\\
\rm{rot}\boldsymbol{B} &= \mu_0 \boldsymbol{i} + \frac{1}{c^2}\frac{\partial \boldsymbol{E}}{\partial t}
\end{align}
ここで、はそれぞれ電荷密度、電流密度で、点電荷のときはデルタ関数で表せる。
上からそれぞれ、
・ガウスの法則(Gauss's law)
・磁場のガウスの法則(Gauss's law for magnetism)
・ファラデーの電磁誘導の法則(Faraday's law of induction)
・アンペール・マクスウェルの法則(Ampère's circuital law with Maxwell's addition)
と呼ばれる。
二番目の式は磁束保存の式ともいわれる。
百聞は一見にしかずというのなら、百見は一方程式にしかずともいうべきか、第一式は電束密度の発散が電荷密度そのものであることを示し、第二式は磁気モノポールが存在しない(磁束の湧き出しがない)こと、第三式は磁束密度(磁場)の時間変化に伴って渦のように電場が生じること、そして第四式は同様に電束密度の時間変化に伴ってだけでなく電流さえあれば磁場は発生するのだということを示している。
しかし、磁気単極子の存在についてはいまだスーパーカミオカンデなどで観測が試みられていたり、1931年にディラックがその存在を仮定した上で上式とは別の形のマクスウェルの方程式を導出していたり、それはそれで奥深かったりするので一概に今知られている物理法則が絶対に正しいとは信用しては行けないようだ。といっても、私達の生活環境において近似的に成り立っていることには変わりない。
もし磁気モノポールが存在するなら、磁荷が電磁場から受け取る力は
となるらしく、ローレンツ力と比較してもまさに電場と磁場が双対な関係であることが見て取れる。もしそうだとしたら、この世界は対称的でなんて美しいことだろうか? それともそれはただの対称性という甘い蜜に吸い寄せられる学者への罠で、世界は非対称であることを前提としているのか? そもそも対称であることは完全なのか? なぜ人間は対称であることを求めるのか? 理解するのが楽だから? 確かに、非対称であるよりは、対称である事の方が確率が低く、従って対称であるようにして導かれた双対の関係は真である可能性が高い。しかしだからといって、それが絶対に真である必然性はない。
また平成24年の首都大学東京のPDFで、理論的に磁気モノポールを実験室で作れることを示したと書かれているが、なぜか記載されている原論文のURLが無効で真贋の確認ができなかった。*3
電磁ポテンシャル、ゲージ変換
電磁ポテンシャル
任意の空間ベクトルで、
が計算によってわかる。
なので磁場のガウスの法則(磁束保存の式)から、とおける。
よって、ファラデーの電磁誘導の法則は
\begin{align}
\rm{rot}\boldsymbol{E} + \frac{\partial \boldsymbol{B}}{\partial t}=\rm{rot}\left(\boldsymbol{E} + \frac{\partial \boldsymbol{A}}{\partial t} \right) = 0\tag{1}
\end{align}
となるが、とおくと、これは静電ポテンシャル
の一般化となっており、また
を満たす。
の組を「電磁ポテンシャル(Electromagnetic vector potential)」という。
ここで、より、ガウスの法則は
\begin{align}
-\rm{div}\boldsymbol{E}=\Delta\phi+\rm{div}\frac{\partial \boldsymbol{A}}{\partial t}=-\frac{\rho}{\varepsilon_0}
\end{align}
となる。また、が成分の計算で分かるから*4、アンペール・マクスウェルの法則は
\begin{align}
\rm{grad}\ \rm{div}\ \boldsymbol{A}-\Delta\boldsymbol{A}=\mu_0\boldsymbol{i}+\frac{1}{c^2}\frac{\partial}{\partial t}\left(-\rm{grad}\ \phi-\frac{\partial \boldsymbol{A}}{\partial t}\right)
\end{align} \begin{align}
\left(\Delta - \frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\boldsymbol{A} - \rm{grad}\left(\rm{div}\boldsymbol{A}+\frac{1}{c^2}\frac{\partial}{\partial t}\phi\right)=-\mu_0 \boldsymbol{i}
\end{align}
と変形できる。以上をまとめると
\begin{align}
\Delta\phi+\rm{div}\frac{\partial \boldsymbol{A}}{\partial t}=-\frac{\rho}{\varepsilon_0}\tag{2}
\end{align}\begin{align}
\left(\Delta - \frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\boldsymbol{A} - \rm{grad}\left(\rm{div}\boldsymbol{A}+\frac{1}{c^2}\frac{\partial}{\partial t}\phi\right)=-\mu_0 \boldsymbol{i}\tag{3}
\end{align}\begin{align}
\boldsymbol{B}=\rm{rot}\boldsymbol{A},\ \boldsymbol{E}=-\rm{grad}\ \phi - \frac{\partial \boldsymbol{A}}{\partial t}
\end{align}
となる。
ゲージ変換
ここで、任意の空間ベクトルに対して
が成り立つから、
は、変換
に対して不変(invariant)である。このとき
とすると、
に対しても不変にできる。この電磁ポテンシャルの変換を「ゲージ変換(Gauge transformation)」という。
ここで、
\begin{align}
\rm{div}\boldsymbol{A}+\frac{1}{c^2}\frac{\partial}{\partial t}\phi=\rm{div}\boldsymbol{A^{\prime}}+\frac{1}{c^2}\frac{\partial}{\partial t}\phi^{\prime}+\left(\Delta-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\chi
\end{align}
であるから、
\begin{align}
\left(\Delta-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\chi=-\rm{div}\boldsymbol{A^{\prime}}-\frac{1}{c^2}\frac{\partial}{\partial t}\phi^{\prime}
\end{align}
とすれば、式の第2項を0にすることができ、つまり、
\begin{align}
\rm{div}\boldsymbol{A}+\frac{1}{c^2}\frac{\partial}{\partial t}\phi=0
\end{align}
(ローレンツ条件)を得るので、式は
\begin{align}
\left(\Delta - \frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\boldsymbol{A}=-\mu_0 \boldsymbol{i}
\end{align}
となる。また式にローレンツ条件を適用すると、
\begin{align}
\left(\Delta - \frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\phi=-\frac{\rho}{\varepsilon_0}
\end{align}
であるから、上記をまとめて「ローレンツゲージにおけるマクスウェルの方程式」
\begin{align}
\begin{cases}
&\left(\Delta - \frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\phi=-\frac{\rho}{\varepsilon_0}\\
& \left(\Delta - \frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\boldsymbol{A}=-\mu_0 \boldsymbol{i}\\
& \rm{div}\boldsymbol{A}+\frac{1}{c^2}\frac{\partial}{\partial t}\phi=0
\end{cases}
\end{align}
を得る。
尚、四元ポテンシャル(Electromagnetic four-potential)、四元電流密度(Four-current)
、ダランベルシャン(d'Alembertian)
を用いて、上2式は
\begin{align}
\therefore\ \Box A^{\mu}=\mu_0 \boldsymbol{J}
\end{align}
と簡略化できる。
\begin{align}
\end{align}
*1:懐かしいと言っても結局は1年前とかそんなもんなんだけど、貧乏には変わりなかったけど稼ぐためにただひたすらアプリ開発をしていて、あまりにも精神的にきつかったためコーディングしながらドラマを見ていた。アプリの設計図を作ったらそれを壁に貼ることで、あまりアプリ開発に集中しなくてもコードが書けるのだ。3Dモデリングをしているときも同じ要領で、それでドラマを20〜30本、映画を300本くらい見た。もし人生が有限でなかったなら、世の中にあるすべての映画・ドラマ・小説をみたいし、これまでの全ての歴史を知りたい。しかし実際には、無限という存在からするとそのような情報を得る膨大な時間でさえも限りなく矮小である。とはいえどの道全ての歴史を知ることはできない。なぜなら始皇帝の時代に焚書された書物、チンギスハンによって侵略された国の書物などそもそもこの世から消えてしまった本が多くある上に、革命によって打倒された王朝は史実を歪めてまで貶される傾向にあったり、新約聖書など後世になって政治的な都合によって盛られたりといった例もあるので、どこまで信用していいかわからないものも多い。したがってタイムマシンの開発が待たれる。
*2:はじめアルゴリズムという漫画の主人公がまさにそんな感じだった。まだ1巻しか買えてない
*3:しかも(もし本当であれば)すごい結果であるにも関わらず、「磁気モノポール 首都大学東京」で調べてもなぜか当時の記事や2chの掲示板しかヒットせず10年たっても目新しい情報が出ていないということは、多分結果が間違いだったか、誰かが実在の教授などの名前を借りて巧妙なイタズラ記事を作っただけなのかもしれない。(最初は全部ウソだと思ったけど、教授の名前とか電話番号は本物なんだよなあ......)
*4:成分の計算でも分かるが、パッと思い出したいときに使える考え方がある。平行でない空間ベクトルについて、
は
に対して垂直であり、
はその
に対して垂直であるため結局この3重積は
に対して同一平面上に存在する。したがって、スカラー
で
となるものが存在する。両辺に
を内積すると
より、スカラー
で
とおけるが、
に適当な特殊値を代入して
であるとわかる。これにより、
\begin{align}
\boldsymbol{a}\times(\boldsymbol{b}\times\boldsymbol{c})=(\boldsymbol{a}\cdot\boldsymbol{c})\boldsymbol{b}-(\boldsymbol{a}\cdot\boldsymbol{b})\boldsymbol{c}
\end{align}
が成り立つ。また、右辺を並び替えることでアルファベットが「バック・キャブ(bac cab)」となるというカスみたいな覚え方もある。
デルタ関数をガンマ関数で微分すると反復指数になる

は積分すると初等関数で表せるのに、
を積分すると高等関数になるのはなぜか。
同様に、は積分すると初等関数で表せるのに、
の積分は高等関数になるのはなぜか、それは指数が一段階増えるごとに全く別の世界になるからである。*1
話は変わるが私は前に一度数学の世界を抜け出して、今までエンジニアとしてディープラーニングを含むITの技術を学習したり3Dゲームを作ったりしてきたが今頃になって、大学数学と物理を勉強し直している。といっても怪しげなものでなく、しっかり大学のカリキュラムに則って自分で参考書を買って超弦理論やM理論を目指して独学している。あとMIT、そしてNASAに入りたい。
研究らしい研究はブログに書けないくらい長くなっちゃうので、このブログではメモ代わりにちょっとした思いつきというかすぐに忘れそうだけどおもしろい自由研究みたいなものを書きたい。
ヘヴィサイドの演算子法において、とする。
このときの関数
に対して
\begin{align}
e^Df(x)=f(x+1)
\end{align}
はよく知られた事実だ。これは左辺のが、 関数を1だけずらす並進作用素であると捉えることもできる。
いちおう過程を示しておくと、
\begin{align}
e^Df(x)=\left(\sum^{\infty}_{n=0}\frac{D^n}{n!}\right)f(x)=\sum^{\infty}_{n=0}\frac{f^{(n)}(x)}{n!}
\end{align}
ここで右辺は、を
についてテイラー展開したものに
を代入したものであるので、
となるわけだ。
さっきはのことをただ関数とだけ述べたが、上式では無限階微分にまで考えているので、必然的に
は
級であることが要請される。
また同様に、もわかる。これはつまり、逆に
が
でさえあれば、形式的にでも
という演算子が並進作用素の役割を担う記号であると認識できるのではないだろうか。
ならば、指数関数だけでなく、高等関数のようなものを使ってみたらどうなるのだろう?
上記では並進について述べることができたが、もしかしたら考える関数によってたとえば回転、発散、加算、乗算、冪、テトレーションなどの演算を、とある微分の関数を使って表せることができるかもしれない。仮にすべての演算に対してそのような関数があるならその対応関係からなにかさらに発展した事柄に結べつけられそうな気もするが、微分というものが果たしてそこまで本質的なのだろうか。なぜ、曲線の傾きを求めようとして始まった微分という演算が、数学の中で解析学という一大分野を築き上げるほど深遠な性質を持たなければならなかったのか。なぜ人類は、ニュートン及びライプニッツが微積分を発明してからこの数百年間、この演算子に縛られ続けているのだろうか。分数階微分学や、擬微分作用素というものはあるが、微分という概念を超える画期的な「何か」はないのか。それとも、その「何か」が代数学や幾何学といったものなのだろうか。千年後、二千年後の人類は、一体どんな数学を扱っているのだろう。
いつもそんなことが気になって仕方がない。
...というのはただの独り言で、下記とは関係ない。
ここでガンマ関数
\begin{align}
\Gamma(s):=\int^{\infty}_{0}e^{-t}t^{s-1}dt
\end{align}
のの部分に微分演算子
を入れて関数を作用させてみると、
\begin{align}
\Gamma(D)f(x)&=\int^{\infty}_{0}e^{-t}t^{D-1}dt f(x)\\
&=\int^{\infty}_{0}e^{-t}e^{(\log t) D}f(x)\frac{dt}{t}\\
&=\int^{\infty}_{0}e^{-t}f(x+\log t)\frac{dt}{t}\\
&=\int^{\infty}_{-\infty}f(x-t)e^{-e^{-t}}dt\\
\end{align}
ここで、最後の行でという変数変換を行っている。
また、畳み込み積分の定義
\begin{align}
(f*g)(x)=\int^{\infty}_{-\infty}f(x-t)g(t)dt
\end{align}
より最後の式は、反復指数函数(
個の
の上に
が乗っている)を使うと
\begin{align}
\Gamma(D)f(x)=(f*\exp^2_{1/e})(x)\tag{1}
\end{align}
と表せる。つまり、ガンマ関数で微分するとその関数は、その関数と反復指数との畳み込み積分に変換されるということになる。ただ反復指数の部分に関してはを反復するか
を反復するかという違いしかないので、添字部分にわざわざ
などと書くのは気が引ける。なので反転(Reversed)反復指数関数なるものをつくってそれを
もしくは
とでも表記してやればスマートにかけるのだが、あくまでも自由研究の範囲なので面倒なことはしたくないし、胡散臭さに拍車がかかってしまいそうなのが嫌だ。
とにかく、微分演算子の世界においては、ガンマ関数に反復指数の畳み込みが対応しているというところが本質なのだと思う。
一方で、畳み込み積分においては、次のような等式が成り立つ。
\begin{align}
F[f*g]=F[f]F[g]
\end{align}
ここではフーリエ変換。
いちおうこの式を示しておくと、
\begin{align}
F[(f*g)(x)]&=\int^{\infty}_{\infty}(f*g)(t)e^{-2\pi i xt}dt\\
&=\int^{\infty}_{\infty}\int^{\infty}_{\infty}f(t-u)g(u)e^{-2\pi i xt}dudt\\
&=\int^{\infty}_{\infty}\int^{\infty}_{\infty}f(t)e^{-2\pi i xt}g(u)e^{-2\pi i xu}dudt\\
&=F[f(x)]F[g(x)]
\end{align}
である。
したがって、式の両辺をフーリエ変換してみると右辺は畳み込みであるので
\begin{align}
F[\Gamma(D)f(x)]=F[f(x)]F[e^{-e^{-x}}]
\end{align}
となる。ここで反復指数の部分を、わかりやすいように元の式に戻しておいた。というか、写像として書くならとして、それを値として書くなら
としてという便宜上の問題なのだ。
ところで、ディラックのデルタ関数のフーリエ変換は1になることは定義からしても明らかであるが、デルタ関数をこの式に代入してみると
\begin{align}
F[\Gamma(D)\delta(x)]=F[\delta(x)]F[e^{-e^{-x}}]=F[e^{-e^{-x}}]
\end{align}
というふうに、両辺がともにフーリエ変換された状態に変形できる。よって両辺をフーリエ逆変換して
\begin{align}
\therefore\ \Gamma(D)\delta(x)=e^{-e^{-x}}
\end{align}
という式を得る。
タイトル通り言いたかったことはこれだけなのだが、長々説明してしまった。これはつまり、デルタ関数をガンマ関数で微分すると反復指数になるということであるが、はたして本当にこれは成り立つのだろうか? 成り立つとして、ここからなにか有用な結果を導くことができるのだろうか?
ちなみに、 は以下のようなシグモイド型の単調なグラフになる。

だが、冒頭でも述べたとおりこれを(不定)積分しようものならそれは高等関数になる。厳密にはリゥヴィルの判定法という、ある積分が初等関数で表せるかどうかを判定する方法がありそれでわかるのだが、この積分に関しては指数積分というれっきとした名のついた高等関数に変形できる。
したがって、
\begin{align}
\int^{1}_{0}e^{-e^{-x}}dx\tag{2}
\end{align}
という、一見なんとかこねくり回せば解けそうな積分も結局は閉じた式で書き表すことはできない。積分範囲に理由はない、というか被積分関数からすると不自然な範囲だろう。
余談だが、私は中学二年のときに、東大の文化祭に行ってそこの数学科で開催されていた積分100問を早く解く大会みたいなので優勝したことがあるほど、積分が得意である。ちなみに2位は数学科の人で、大差をつけて自分が勝った。だから大抵の積分は見ただけで解けるかどうかわかる(解が分かるとはかぎらない。。。)のだが、上式のように一見解けそうで解けないというのがもどかしい。
余談に余談だが、つい最近
\begin{align}
\int^{1}_{0}\log \Gamma(t)dt
\end{align}
という積分が解ける(というか解が知られている)ことを知った。相反公式を使うと解ける。
具体的には、
\begin{align}
\int^{1}_{0}\log \Gamma(t)dt&=\int^{1}_{0}\log \Gamma(1-t)dt\\
&=\int^{1}_{0}\log\left(\frac{\pi}{\sin\pi t}\right) - \int^{1}_{0}\log \Gamma(t)dt\\
&=\frac{1}{2}\left(\log\pi - \int^{1}_{0}\log\sin(\pi t) dt\right)
\end{align}
ここで、や、
、
などの三角関数の基本的性質を駆使すると
\begin{align}
\int^{1}_{0}\log\sin(\pi t) dt &=\int^{1/2}_{0}\log\sin(\pi t) dt + \int^{1}_{1/2}\log\sin(\pi t) dt\\
&= 2\int^{1/2}_{0}\log\sin(\pi t) dt\\
&= 2\int^{1/2}_{0}\log\frac{\sin 2\pi t}{2 \cos \pi t} dt\\
&= -\log 2 + \int^{1}_{0}\log\sin(\pi t) dt - 2\int^{1/2}_{0}\log\sin(\pi t) dt\\
&= -\log 2
\end{align}
が分かる。最後から二番目の式の第2項と第3項は、それぞれ一行目の左辺と右辺であるので、きれいに打ち消されている。
これにより
\begin{align}
\int^{1}_{0}\log \Gamma(t)dt=\frac{1}{2}\log(2\pi)
\end{align}
となる。なんともきれいな結果だ。
そうして、もう一度式を見てみよう。ねんのため再掲しておく。
\begin{align}
\int^{1}_{0}e^{-e^{-x}}dx
\end{align}
なんでさっきの積分が解けてコレがとけないんだ!?という気がしてこない? え、当然? あ、そう。まあどっちでもいんだけど。
このような一連の結果が示唆することとは、つまり積分するという行為の上では指数〜多項式〜対数レベルの世界ではおおよそ初等関数で表せるが、一度その世界から足を踏み外してしまうと、それまでの常識が通用しなくなるということなのだ。
この観点を踏まえると、
\begin{align}
\int^{1}_{0}e^{-e^{-x}}dx&=\int^{1}_{0}\Gamma(D)\delta(x)dx
\end{align}
というのは、それまでの常識を打ち破る何かを秘めているようにも見えてくる。
たとえば、
\begin{align}
\int^{1}_{-1}D \delta(x)dx = [\delta(x)]^{1}_{-1}=0
\end{align}
であろうから、と
とのあいだに生ずる歪みのようなものを取っ払ってやれば、上の式も解けるのではないか、、、という淡い期待を抱かざるを得ない。
しかしながら、多分これ以上の詮索はあまり意味がないと思う。
もし画期的ななにかがあるとしても、それはここから生まれるものではなくてもっと上位の概念から生まれる高度なものに違いない。新しい概念を生み出すことは全くもって容易ではない。現在地球上に80億人いて1000年分の人口が集まっていると言われている中、それぞれの分野においてかつてないほどの競技人口がひしめき合い、今も世界のどこかで自分より頭のいい人たちが何かを変えようとして必死に頑張っている。そんな中で、いち素人が現状のまま成功できるだろうという考えは甘すぎる。
だから今自分ができることは、とにかく最新の数学・物理学を習得するまで努力研鑽し続けることだ。
とはいったものの、このままではなんとなく物足りないため、最後にちょっと変わった面白い等式を紹介したいと思う。上のことについて考えていたときについでに自分で導いたものなんだけど、すでにガウスかオイラーあたりがやっていそうで怖い。てか、やってるだろうな。
反復指数に関する積分
\begin{align}
\int^{\infty}_{-\infty}e^{-x}e^{-e^{-x}}\left(1-e^{-e^{-e^{-x}}}\left(1-e^{-e^{-e^{-e^{-x}}}}\left(\cdots \right)\right)\right) dx = \Omega
\end{align}
ここではランベルトのオメガ定数
。
証明.
とする。
まず無限テトレーションの収束 | Mathlogで示されている通り、のとき
は収束するから、
も収束し、
で与えられる。
またのとき、
である。
次に、合成関数の微分から、
\begin{align}
\frac{d}{dx}\rm{rex}^{n}(x)=\left(-\frac{d}{dx}\rm{rex}^{n-1}(x)\right) \cdot \rm{rex}^{n}(x)=(-1)^n \prod^n_{k=1}\rm{rex}^k(x)
\end{align}
が分かるから、右辺を積分することで、
\begin{align}
\int^{\infty}_{-\infty}(-1)^n \prod^n_{k=1}\rm{rex}^k(x)dx &= \int^{\infty}_{-\infty} \frac{d}{dx}\rm{rex}^{n}(x) dx \\
&=\rm{rex}^{n}(\infty)-\rm{rex}^{n}(-\infty)\\
&=\rm{rex}^{n-1}(0)-\rm{rex}^{n-2}(0)
\end{align}
一方、三行目についての範囲で和を取るとこれはtelescoping series(望遠鏡級数)であり、和が徐々に打ち消されて
になる。
またのとき任意の実数
について
であることは容易に分かるので、
とすると、
は単調減少で
を満たすから、交代級数
はAlternating series testを満たし、収束する。これにより総和記号と積分の入れ替えが可能となり
\begin{align}
\Omega &= \int^{\infty}_{-\infty}e^{-x}e^{-e^{-x}}-e^{-x}e^{-e^{-x}}e^{-e^{-e^{-x}}}+e^{-x}e^{-e^{-x}}e^{-e^{-e^{-x}}}e^{-e^{-e^{-e^{-x}}}}+\cdots dx\\
&=\int^{\infty}_{-\infty}e^{-x}e^{-e^{-x}}\left(1-e^{-e^{-e^{-x}}}\left(1-e^{-e^{-e^{-e^{-x}}}}\left(\cdots \right)\right)\right) dx
\end{align}
を得る。
\begin{align}
\end{align}
ζ(2k+1) の漸化式
\begin{align}
&\xi_k := \frac{(-1)^{k - 1}(2\pi)^{2k}}{(2k)!(2^{2k+1}-1)}\\
\\
&\xi(2k+1) := \frac{1}{\xi_k} \zeta(2k+1)\\
\\
&\theta_k := \frac{2^{2k} - 1}{2^{2k+1} - 1}\\
\\
&s_k := 2^{2k}\log\mathcal{S}_{2k+1}(1/2)
\end{align}
と定義すると、
\begin{align}
\xi(2k+1) = \log 2 - s_k - \sum^{k - 1}_{m = 1}
\left(
\begin{array}
\ 2k \\
2m
\end{array}
\right)
\theta_m \xi(2m + 1)
\end{align}
が成り立つ。ここでとは多重三角関数のことで、
\begin{align}
\mathcal{S}_r(x) &:= e^{\frac{x^{r - 1}}{r - 1}}\prod_{l\in \mathbb{Z}_{\neq 0}}P_r(x/l)^{l^{r - 1}}\\
P_r(x) &:= (1-x)\exp\left\{\sum^{r - 1}_{k = 1}x^k / k\right\}
\end{align}
である。
Lemmas
1
Lemma_1
複素数に対し、
\begin{align}
\sum^{\infty}_{n=1}\frac{(-1)^{n - 1}}{n^s} = (1 - 2^{1 - s})\zeta(s)
\end{align}
\begin{align}
\sum^{\infty}_{n=1}\frac{(-1)^{n - 1}}{n^{s}} &= 1 - \frac{1}{2^s} + \frac{1}{3^s} - \frac{1}{4^s} + \cdots\\
&= \left(1 + \frac{1}{2^s} + \frac{1}{3^s} + \frac{1}{4^s} + \cdots\right)\\
& - 2\left(\frac{1}{2^s} + \frac{1}{4^s} + \cdots\right)\\
&= \zeta(s) - 2^{1-s}\zeta(s) = (1 - 2^{1 - s})\zeta(s)
\end{align}
2
Lemma_2
\begin{align}
\sum^{\infty}_{n=1}\frac{(-1)^{n-1}}{n} = \log 2
\end{align}
リーマンゼータ関数の極はで一位であり、留数は1と知られているので
Lemma_1を用いて。もしくは純粋に
\begin{align}
\log (1 + x) = \sum^{\infty}_{n=1}\frac{(-1)^{n - 1}}{n}x^n
\end{align}
より求まる。
2.5
Lemma_2.5
なら、
\begin{align}
a &= ba +c \\
&= \frac{c}{1-b}
\end{align}
3
Lemma_3
\begin{align}
\zeta(- k) = -\frac{B_{k+1}}{k+1}
\end{align}
ここではベルヌーイ数。ベルヌーイ数とは、
\begin{align}
\frac{x}{e^x - 1} = \sum^{\infty}_{n=0}\frac{B_n}{n!}x^n
\end{align}
となる数のことで、ならば
である。
4
Lemma_4(named: "反復積分に関するコーシーの公式")
実数を起点とする
回の不定積分を考える。積分演算子を
とし、
が
で連続であるとき、
\begin{align}
J^n f(x) :&= \int^{x}_{x_0}\int^{t_{n - 1}}_{x_0}\cdots\int^{t_1}_{x_0}f(t_0)dt_0\cdots dt_{n - 1}\\
&= \frac{1}{(n - 1)!}\int^{x}_{x_0}(x - t)^{n - 1}f(t) dt
\end{align}
が成り立つ。
帰納法で示す。のとき明らかに正しい。
のときに成り立てば、
\begin{align}
J^{n+1}f(x) &= \int^{x}_{x_0}J^n f(t)dt\\
&= \int^{x}_{x_0}\frac{1}{(n - 1)!}\int^{t}_{x_0}(t - u)^{n - 1}f(u)dudt\\
&= \frac{1}{(n - 1)!}\int^{x}_{x_0}\int^{x}_{u}(t - u)^{n - 1}f(u)dtdu\\
&= \frac{1}{n!}\int^{x}_{x_0}(x - u)^n f(u)
\end{align}
となり確かに正しい。
5
Lemma_5
\begin{align}
\mathcal{S}_k(x)=\exp\left\{\int^{x}_{0}\pi t^{k - 1}\cot(\pi t)dt\right\}
\end{align}
定義式
\begin{align}
\mathcal{S}_k(x) &:= e^{\frac{x^{k - 1}}{k - 1}}\prod_{l\in \mathbb{Z}_{\neq 0}}P_k(x/l)^{l^{k - 1}}\\
P_k(x) &:= (1-x)\exp\left\{\sum^{r - 1}_{k = 1}x^k / k\right\}
\end{align}
を対数微分すると、右辺はとなる。一方、三角関数の因数分解(っぽいやつ)
\begin{align}
\sin(\pi x) = \pi x\prod_{l\in\mathbb N}\left(1-\frac{x^2}{l^2}\right)
\end{align}
を対数微分すると、
\begin{align}
\pi \cot(\pi x) = \sum_{l\in \mathbb Z}\frac{1}{x - l}
\end{align}
となる。であるから、
\begin{align}
\mathcal{S}_k(x) = \exp\left\{\int^{x}_{0}\pi t^{k - 1}\cot(\pi t)dt\right\}
\end{align}
である。
Proof
は、それが使われている式と上の式の間で、
Lemma_nを使ったことを意味する。
\begin{align}
\zeta(2k+1):&=\sum^{\infty}_{n=1}\frac{1}{n^{2k+1}}\\
&=
\sum^{\infty}_{n=1}\frac{(-1)^n}{n^{2k+1}}\cos(\pi n)\\
&=
\sum^{\infty}_{n=1}\frac{(-1)^n}{n^{2k+1}}\sum^{\infty}_{m=0}\frac{(-1)^m}{(2m)!}\pi^{2m}n^{2m}\\
&=
-\sum^{\infty}_{m=0}\frac{(-1)^m}{(2m)!}\pi^{2m}\sum^{\infty}_{n=1}\frac{(-1)^{n - 1}}{n^{2k+1-2m}}\\
&\stackrel{1}{=}
- \sum^{\infty}_{m=0}\frac{(-1)^m}{(2m)!}\pi^{2m}(1-2^{2m - 2k})\zeta(2k + 1 - 2m)\\
&=
-\left(\sum_{0≤m\lt k} + \sum_{m = k} + \sum_{m \gt k}\right)\text{中身} \\
&\stackrel{2}{=}
-(1-2^{-2k})\zeta(2k+1)-\sum^{k - 1}_{m=1}\frac{(-1)^{k - m}}{(2k - 2m)!}\pi^{2k - 2m}(1 - 2^{-2m})\zeta(2m+1)\\
& \ \ \ \ - \frac{(-1)^k}{(2k)!}\pi^{2k}\log 2\\
& \ \ \ \ - \sum^{\infty}_{m=1}\frac{(-1)^{m + k}}{(2m + 2k)!}\pi^{2m + 2k}(1 - 2^{2m})\zeta(1 - 2m)\\
&\stackrel{2.5,\ 3}{=}
\xi_k
\left \{
\begin{array}
\ \log 2 \\
- \sum^{k - 1}_{m=0}
\left(
\begin{array}
\ 2k\\
2m
\end{array}
\right)
\theta_m \xi(2m + 1)\\
- (2k)!\sum^{\infty}_{m = 1}\frac{(-1)^{m - 1}B_{2m}}{2m(2m + 2k)!}( (2\pi)^{2m} - \pi^{2m})
\end{array}
\right\}
\end{align}
\begin{align}
&\xi_k := \frac{(-1)^{k - 1}(2\pi)^{2k}}{(2k)!(2^{2k+1}-1)}\\
\\
&\xi(2k+1) := \frac{1}{\xi_k} \zeta(2k+1)\\
\\
&\theta_k := \frac{2^{2k} - 1}{2^{2k+1} - 1}
\end{align}
では次に、最後の行の、最後の項を母関数の特殊値として表現する。
\begin{align}
- (2k)!\sum^{\infty}_{m = 1}\frac{(-1)^{m - 1}B_{2m}}{2m(2m + 2k)!}( (2\pi)^{2m} - \pi^{2m})=-(2k)!(f(2\pi) - f(\pi) )
\end{align}
つまり、
\begin{align}
f(x) := \sum^{\infty}_{m = 1}\frac{(-1)^{m - 1}B_{2m}}{2m(2m + 2k)!}x^{2m}
\end{align}
である。これを微分してをかけたものを
とおくと、
\begin{align}
g(x):= x^{2k+1}f^{\prime}(x) = \sum^{\infty}_{m = 1}\frac{(-1)^{m - 1}B_{2m}}{(2m+2k)!}x^{2m+2k}
\end{align}
次に、これを回微分したものを
とすると、
\begin{align}
h(x) := g(2k)(x) = \sum^{\infty}_{m=1}\frac{(-1)^{m - 1}B_{2m}}{(2m)!}x^{2m}
\end{align}
なので、ベルヌーイ数の定義
\begin{align}
\frac{x}{e^x - 1} &= \sum^{\infty}_{m = 0}\frac{B_m}{m!}x^m\\
&= 1 - \frac{1}{2}x + \sum^{\infty}_{m = 1}\frac{B_{2m}}{(2m)!}x^{2m}
\end{align}
より、
\begin{align}
h(x) &= 1 - \frac{1}{2}ix - \frac{ix}{e^{ix} - 1}\\
&= 1 - \frac{x}{2}\cot\left(\frac{x}{2}\right)
\end{align}
よって、Lemma_4(named: "反復積分に関するコーシーの公式")(なので積分の起点は0)より、
\begin{align}
g(x) &= \int\cdots\int \left(1 - \frac{x}{2}\cot\left(\frac{x}{2}\right)\right)d^{2k}x\\
&= \frac{x^{2k}}{(2k)!} - \int\cdots\int \frac{x}{2}\cot\left(\frac{x}{2}\right) d^{2k}x\\
&= \frac{1}{(2k)!} \left\{ x^{2k} - 2k\int^{x}_{0} (x - t)^{2k - 1}\frac{t}{2}\cot\left(\frac{t}{2}\right)dt \right\}\\
&= \frac{x^{2k}}{(2k)!}\left\{1 - 2kx\int^{1}_{0}(1 - t)^{2k - 1}\frac{t}{2}\cot\left(\frac{xt}{2}\right)dt\right\}
\end{align}
で、
\begin{align}
f(x) &= \int \frac{1}{x^{2k + 1}}g(x)dx\\
&= \frac{1}{(2k)!}\left\{\log x - 2k \int^{1}_{0}(1-t)^{2k - 1}\log \sin\left(\frac{xt}{2}\right)dt\right\}
\end{align}
そして、元々考えていたとは、つまり
より、
\begin{align}
\ -(2k)!(f(2\pi)-f(\pi) ) &= -\log 2 + 2k\int^{1}_{0}(1 - t)^{2k - 1}\left(\log 2 + \log\cos\left(\frac{\pi t}{2}\right)\right)dt\\
&= 2k\int^{1}_{0}(1 - t)^{2k - 1}\log\cos\left(\frac{\pi t}{2}\right)dt\\
&= - \int^{1}_{0}\frac{\pi}{2}(1 - t)^{2k}\tan(\pi t / 2)dt\\
&= -\int^{1}_{0}\frac{\pi}{2}t^{2k}\cot(\pi t/2)dt\\
&= -2^{2k}\int^{1/2}_{0}\pi t^{2k}\cot(\pi t)dt\\
&\stackrel{5}{=}-2^{2k}\log\mathcal{S}_{2k+1}(1/2)\\
&= -s_k
\end{align}
となる。上記をまとめると、
\begin{align}
\zeta(2k+1) = \xi_k\left(\log 2 - s_k - \sum^{k - 1}_{m = 1}
\left(
\begin{array}
\ 2k\\
2m
\end{array}
\right)
\theta_m \xi(2m + 1)
\right)
\end{align}
なので、
\begin{align}
\xi(2k+1) = \log 2 - s_k - \sum^{k - 1}_{m = 1} {}_{2k} C _{2m} \theta_m \xi(2k+1)
\end{align}
□
多項間漸化式の母関数

調べても出てこないのでメモ。というか基本理念として、調べても出てこないものばかり記事にする。そもそも、収益や閲覧数を目的としていないのでそれは必然的だ。
また、昨日家に出現したゴキブリを退治しようとしたところ、右手中指を骨まで切断。金がないので病院に行けず、応急措置を誤ったため断層が発現し、多分なにもしなければ二度と元どおりには治らない。そのため、4本指のタイピングが上手くなる。
多項間漸化式の解
項間漸化式
\begin{align}
a_{n + k - 1}=\sum^{k - 2}_{m = 0}b_m a_{n + m}
\end{align}
の母関数は
\begin{align}
F(x) &:= \sum^{\infty}_{n = 0}\frac{a_n}{n!}x^n\\
&= \sum^{k - 2}_{m = 0}\frac{P_{k, m + 1}(x)}{P_{k, 0}(x)}a_m x^m
\end{align}
となる。ここで
\begin{align}
P_{k, m}(x)
:=
\begin{cases}
1 - \sum^{k - 2}_{l = m}b_l x^{k - 1 - l} & (m < k - 2)\\
1 & (m = k - 2)
\end{cases}
\end{align}
である。
また、上記ではとしているが、
のように
に依存していてもいい。ただ
にまで依存すると解は別の形になる。(一項間の場合は自明とした。
Proof
まず、級数の中でをくくり出してやる。
\begin{align}
F(x) = \sum^{k - 2}_{n=0}a_n x^n + \sum^{\infty}_{n=k - 1}a_n x^n
\end{align}
右辺第二項は、
\begin{align}
\text{右辺第二項} &= \sum^{\infty}_{n=0}a_{n + k - 1}x^{n + k - 1}\\
&= \sum^{\infty}_{n=0}\sum^{k - 2}_{m=0}b_m a_{n + m}x^{n + k - 1}\\
&= \sum^{k - 2}_{m=0}b_m x^{k - 1 - m}\sum^{\infty}_{n=0}a_{n+m}x^{n+m}\\
&= \sum^{k - 2}_{m=0}b_m x^{k - 1 - m}\left(F(x) - \sum^{m - 1}_{n=0}a_n x^n\right)
\end{align}
であり、これを上式に代入すると
\begin{align}
F(x) = \sum^{k - 2}_{n=0}a_n x^n + \sum^{k - 2}_{m=0}b_m x^{k - 1 - m}\left(F(x) - \sum^{m - 1}_{n=0}a_n x^n\right)
\end{align}
なので右辺のを左辺に移項して係数で割ると
\begin{align}
F(x) = \frac{\sum^{k - 2}_{n=0}a_n x^n - \sum^{k - 2}_{m = 0}\sum^{m - 1}_{n = 0}b_m x^{k - m + n}a_n}{1 - \sum^{k - 2}_{m = 0}b_m x^{k - m}}
\end{align}
となる。であることから、
として右辺分子第二項の和を入れ替える。
\begin{align}
F(x) &= \frac{\sum^{k - 2}_{n=0}a_n x^n - \sum^{k - 3}_{n = 0}\sum^{k - 2}_{m = n + 1}b_m x^{k - m + n}a_n}{1 - \sum^{k - 2}_{m = 0}b_m x^{k - m}}\\
&= \frac{a_{k - 2}x^{k - 2} + \sum^{k - 3}_{n = 0}(1 - \sum^{k - 2}_{m = n + 1}b_m x^{k - m})}{1 - \sum^{k - 2}_{m = 0}b_m x^{k - m}}\\
&= \sum^{k - 3}_{m = 0}\frac{P_{k, m + 1}(x)}{P_{k, 0}(x)}a_m x^m
\end{align}
よって題は示された。□