10x Faster Collatz Calculation

A New Insight into the Collatz Conjecture

In the vast domain of mathematics, the Collatz conjecture holds its unique intrigue. A few days ago, I made an observation that the maximum curve of the Collatz total stopping time bears a resemblance to that of a logarithmic function. This revelation piqued my interest and led me to think: Could there be a more efficient way to calculate the Collatz operation? Traditional methods have been effective in exploring its patterns, but with this new insight, I felt compelled to seek out a method that could potentially expedite the calculations. This article delves into a method that has empirically shown to calculate the Collatz sequence up to 10 times faster than conventional techniques.

Traditional Collatz Sequence Computation

Traditionally, the computation of the Collatz sequence involves the following iterative process:

1. Start with any positive integer n.
2. If n is even, divide it by 2: \begin{align}n \rightarrow \frac{n}{2}\end{align}
3. If n is odd, multiply it by 3 and add 1: \begin{align} n \rightarrow 3n + 1 \end{align}
4. Repeat the process with the new value of n, until n becomes 1.

This method is straightforward but involves many iterations, especially for numbers that require a large number of steps to reach 1. For instance, numbers that take hundreds or even thousands of steps can make the process quite slow. Each step in the process requires a calculation, and as the starting number increases, the potential number of steps can grow significantly. This approach, while effective, can be time-consuming, especially for large numbers and extensive ranges.

This is a sample python code up to N = 1,000,000 (Note that this is originally for verifying my hypotheses):

### Traditional Method
import matplotlib.pyplot as plt
import numpy as np
import time

def collatz(n):
    if n % 2 == 0:
        return int(n/2)
    else:
        return 3*n+1

def collatz_seq(n):
    result = [n]
    while n > 1:
        n = collatz(n)
        result.append(n)
    return result

def plot_collatz(max_n):
    x = list(range(1, max_n))
    y = [len(collatz_seq(i)) for i in x]

    # Filter x and y to keep only points where y is a new maximum
    max_y = 0
    new_x, new_y = [], []
    for i, val in enumerate(y):
        if val > max_y:
            max_y = val
            new_x.append(x[i])
            new_y.append(val)

    # Generate the logarithmic data
    log_y = [3 * np.log(val)**2 for val in x]

    plt.figure(figsize=(10, 6))
    plt.scatter(new_x, new_y, color='blue', label='Collatz Data')
    plt.plot(new_x, new_y, color='blue', marker='o')
    plt.plot(x, log_y, color='red', label='Logarithmic Function')
    plt.title(f"Comparison between Collatz sequences and Logarithmic function (n={max_n})")
    plt.xlabel("Number")
    plt.ylabel("Value")
    plt.grid(True, which='both', linestyle='--', linewidth=0.5)
    plt.legend()
    plt.show()

# Plotting for each value
start_time = time.time()
for n in [1000000]:
    plot_collatz(n)

end_time = time.time()
execution_time = end_time - start_time
print(f"The execution time is {execution_time} seconds.")

This yields:

You can see that this traditional way takes time about 1 minute.

10x Faster Collatz Sequence Computation

One of the foundational elements that has significantly accelerated the computation is the use of caching. In programming, caching is a technique where previously computed results are stored for quicker access in subsequent runs. If the same computations are required again, instead of recalculating them, the program fetches the stored result.

In the given code, caching is achieved using a dictionary named collatz_dic. This dictionary acts as our cache. Whenever we compute the total stopping time for a number n, before moving further in the sequence, the code checks if n already exists in collatz_dic. If it does, it means we have previously calculated the stopping time for that number and we can simply fetch the result from the dictionary instead of recalculating it.

if n in collatz_dic:
  result = collatz_dic[n]
  break

This simple check and retrieval mechanism drastically reduces the computation time as the number of Collatz operations decreases with each known value we encounter.

To ensure that the cache keeps updating and becomes more efficient with every run, new numbers encountered during the calculation, which aren't in the cache, are stored in a list named newNumbers. After the sequence breaks, we populate the collatz_dic with these new numbers and their respective stopping times:

len_newNumbers = len(newNumbers) 
for i in range(1, len_newNumbers):
  result += 1
  collatz_dic[newNumbers[len_newNumbers - i]] = result

By utilizing this approach, the calculation time was observed to decrease significantly, making it up to 10 times faster. This isn't just a theoretical improvement; the reduction in computational time has practical implications, especially for intensive research and larger datasets.

Efficiency in mathematical computations is always a sought-after goal. By exploring alternative methods and continuously refining our approaches, we can uncover more efficient ways to understand and solve problems. The alternative method for the Collatz sequence computation is a testament to this endeavor. While the journey in understanding the Collatz conjecture is far from over, innovations like these bring us a step closer to more profound insights.

This is the sample python code:

import matplotlib.pyplot as plt
import numpy as np
import time

collatz_dic = {}

def collatz(n):
    if n % 2 == 0:
        return int(n/2)
    else:
        return 3*n+1

def collatz_total_stopping_time(n):
  newNumbers = []
  result = 0
  while n > 1:
    if n in collatz_dic:
      result = collatz_dic[n]
      break
    else:
      newNumbers.append(n)
      n = collatz(n)
  
  len_newNumbers = len(newNumbers) 
  for i in range(1, len_newNumbers):
    result += 1
    collatz_dic[newNumbers[len_newNumbers - i]] = result

  return result


def plot_collatz(max_n):
    x = list(range(1, max_n))
    y = [collatz_total_stopping_time(i) for i in x]

    # Filter x and y to keep only points where y is a new maximum
    max_y = 0
    new_x, new_y = [], []
    for i, val in enumerate(y):
        if val > max_y:
            max_y = val
            new_x.append(x[i])
            new_y.append(val)

    # Generate the logarithmic data
    log_y = [3 * np.log(val)**2 for val in x]

    plt.figure(figsize=(10, 6))
    plt.scatter(new_x, new_y, color='blue', label='Collatz Data')
    plt.plot(new_x, new_y, color='blue', marker='o')
    plt.plot(x, log_y, color='red', label='Logarithmic Function')
    plt.title(f"Comparison between Collatz sequences and Logarithmic function (n={max_n})")
    plt.xlabel("Number")
    plt.ylabel("Value")
    plt.grid(True, which='both', linestyle='--', linewidth=0.5)
    plt.legend()
    plt.show()


# Plotting for each value
start_time = time.time()
for n in [1000000]:
    plot_collatz(n)

end_time = time.time()
execution_time = end_time - start_time
print(f"The execution time is {execution_time} seconds.")

This yields:

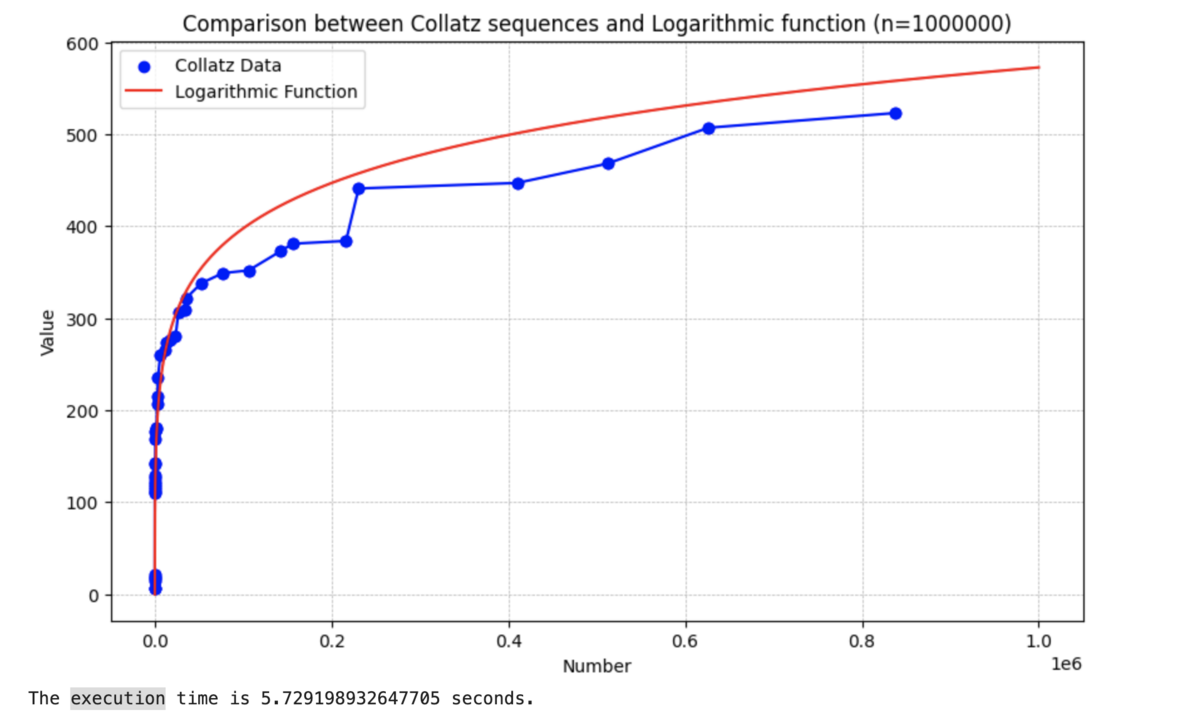
And this only takes 6 seconds. Which is 10 times faster than the traditional way.

Conclusion

The Collatz conjecture, with its seemingly simple rules, continues to puzzle and captivate mathematicians worldwide. Through this article, we've introduced a more efficient computational approach that utilizes caching, which has empirically demonstrated significant speed improvements over traditional methods.

My observation of the curve of the Collatz total stopping time bearing resemblance to the curve of a squared logarithm isn't just a fleeting observation but forms the basis of my hypothesis. It is my fervent hope that someday this hypothesis can be rigorously validated, potentially paving the way for a deeper understanding of the Collatz sequence.

Drawing from the rich theories of zeta functions – a cornerstone of my academic pursuits – and the intricate realms of algebraic structures like Galois theory, I believe we might find clues that will bring us closer to a solution. These mathematical avenues might not only elucidate the Collatz conjecture but also enrich our understanding of the broader tapestry of number theory.

As we continue to unravel the intricacies of the Collatz sequence, the convergence of computational techniques and profound mathematical theories will undoubtedly play a pivotal role. Here's to hoping that the combination of empirical observation, analytic methods, and algebraic structures will someday bear fruit in our quest to decipher the enigma of the Collatz conjecture.